
There are several notations describing infinite compositions, including the following:įorward compositions: F k, n ( z ) = f k ∘ f k + 1 ∘ ⋯ ∘ f n − 1 ∘ f n ( z ). For compositions of a finite number of functions, useful in fractal theory, see Iterated function system.Īlthough the title of this article specifies analytic functions, there are results for more general functions of a complex variable as well. For infinite compositions of a single function see Iterated function. Complex dynamics offers another venue for iteration of systems of functions rather than a single function. It is proved that the set of their shifts has a positive lower density. In addition, it is possible to use ICAF to evaluate solutions of fixed point equations involving infinite expansions. In this paper, a joint approximation of analytic functions by shifts of Dirichlet L-functions L ( s + i a 1 t, 1 ), , L ( s + i a r t, r ), where a 1, , a r are non-zero real algebraic numbers linearly independent over the field Q and t is the Gram function, is considered.

Some functions can actually be expanded directly as infinite compositions. In mathematics, infinite compositions of analytic functions (ICAF) offer alternative formulations of analytic continued fractions, series, products and other infinite expansions, and the theory evolving from such compositions may shed light on the convergence/divergence of these expansions. (example: f(x) = x^3+2*x^2 - 3*x -1 ).Mathematical theory about infinitely iterated function composition How do you find the domain for the composition of two functions, latexfcirc. In previous mathematics courses, we used this idea to determine a formula for the composition of two real functions. This can be referred to as f followed by g and is called the composition of f and g. If the order is reversed when composing two functions, can the result ever be the same as the answer in the original order of the composition If yes, give an example. The basic idea of function composition is that when possible, the output of a function f is used as the input of a function g. However the second part of the problem has me stumped: a) Find functions f, g where g f is bijective but f fails to be onto. I was able to prove this without difficulty. Given the functions f: X Y and g: Y Z, if g f: X Z is bijective, then prove f must be one-to-one and g must be onto. Note that the five operators used are: + (plus), - (minus), / (division), ^ (power) and * (multiplication). What is the composition of two functions, latexfcirc g/latex 3. Composition of two functions - Bijection. It is much similar to addition or multiplication that takes two numbers and gives their sum or product as the output, which is new number. Substitute the variable \( x \) in \( f \) by \( g(x) \)ġ - Enter and edit functions \( f(x) \) and \( g(x) \) and click "Enter Functions" then check what you have entered and edit if needed. The composition of functions is an operation where two functions like f (x) f (x) and g (x) g(x) generate a new function like h (x) h(x) in such a way that we have h (x)g (f (x)) h(x) g(f (x)). Composition is a simple yet powerful operation that takes two functions with one function as the argument for the other and forms a new function. (see digram below).Īccording to the definition above, to find the composition \( (f_o g)(x) \), we substitute the variable of \( f \) by \( g(x) \) 'Function Composition' is applying one function to the results of another: The result of f () is sent through g () It is written: (g f) (x) Which means: g (f (x)) Example: f (x) 2x+3 and g (x) x2 'x' is just a placeholder. 2 - The exponential function is written as (ex). In Maths, the composition of a function is an operation where two functions say f and g generate a new function say h in such a way that h (x) g (f (x)). This composite function is defined if \(x \) is in the domain of \( g \) and \( g(x) \) is in the domain of \( f \). 1 - Enter and edit functions and and click 'Enter Functions' then check what you have entered and edit if needed. Starting from the input \( x \), applying function \( g \) then function \( f \), we end up with a function called the composite function or composition of \( f \) and \( g \) denoted by \( f_o g \) and is defined by
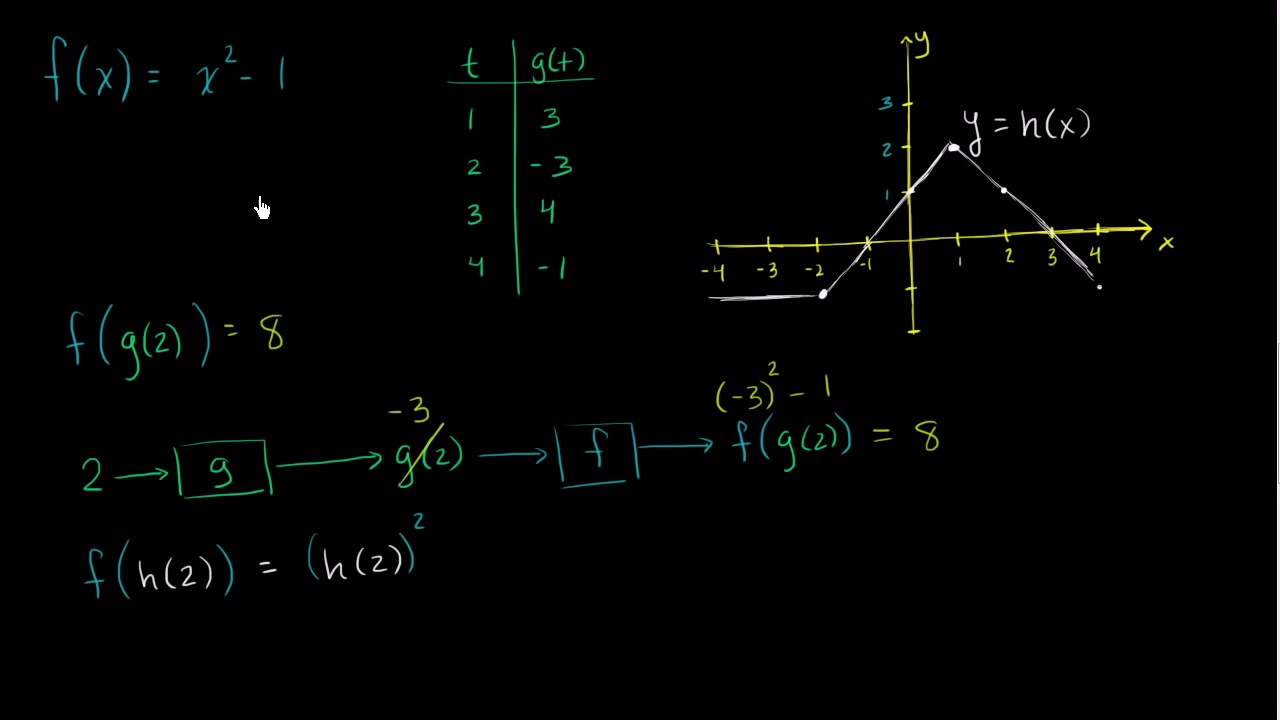
That gets you back to the original input value that you can then use as the input to g (f (x)). In the diagram below, function \( f \) has another function \( g \) as an input. Your function g (x) is defined as a combined function of g (f (x)), so you dont have a plain g (x) that you can just evaluate using 5. A calculator for the composition of functions is presented. Recall that a function is a relation where each element in the domain corresponds to exactly one element in the range.


 0 kommentar(er)
0 kommentar(er)
